I recently listened to a short NPR segment that spoke of why, Humans are bad a making predictions, however Statisticians can do better. One reason for the poor predictions were that people tended to only focus on the details of a problem and derive there prediction afterwards. For example, the speakers proposed that to predict the outcome of a baseball game, non-statisticians would examine factors in pitcher speed, weather, runs, batting average, starting line-ups, and other subtle details with almost no regard to historical game match-ups. This concentration on the small details makes for poor predictions due to the lack of understanding how all of those details were worked on each other, or how they were correlated (and further more, were those details correlated with the outcome prediction). It was proposed that relying on fewer details and historical baseball game match-up would lead to more favorable predictions and statisticians plagued with the numerous details could still construct better predictions.

After this NPR segment I wondered what the statistical underpinnings that were keeping non-statisticians from making better predictions and how this makes a difference in predicting the winner of the game. The seemingly important “details” that should be an indicator of prediction outcome, when added together are in fact an article of over fitting a statistical model. Overfitting means that we are fitting a model to random noise and not correctly describing our underlying relationship. If over fitting has occurred the model can’t be generalized to fit on new data. In the context of machine learning we would fit a model with an algorithm on (most of our data) 99% of our data sample, we would get great training accuracy, but once we tried to test the model on a hold-out sample, the testing accuracy would be poor as we have gone too specific for the model to work well with other data. Over fitting stems from adding many predictors leading to increasing the complexity of the model without improving predictive power.

“Human” misunderstanding about variable correlation is then preceded by including many “details” which may be predictive of each other, known as multicollinearity. A detail about pitching speed and pitch type (i.e. curve ball) could be associated with each other. While multicollinearity does not reduce predictive power or confidence in the model, it can make it difficult to interpret what the model and the individual coefficients mean, as they are not uniquely determined.

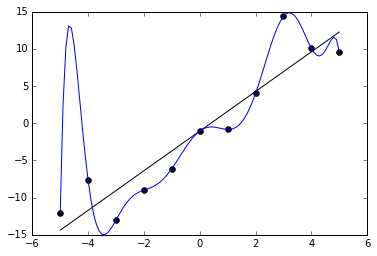
“Noisy (roughly linear) data is fitted to both linear and polynomial functions. Although the polynomial function is a perfect fit, the linear version can be expected to generalize better. In other words, if the two functions were used to extrapolate the data beyond the fit data, the linear function would make better predictions.” - Source: Wikipedia

As Data scientists with experience with building statistical models we have an advantage in assessing our data and performing feature engineering and variable selection so that we can describe all of the “details” which can best explain the most of the variance in the data. Our predictions can be better through understanding statistical importance and aiming for a parsimonious model rather than an overly complicated one.

At the bar when thinking of who will win the World Series or who will win the presidential election it is also importance to consider the bias-variance tradeoff. With over fitting (high variance) previously described as the aggregation of all features with no regard to statistical importance there by making the model sensitive to small fluctuations (or random noise) that it no longer performs well when applied to next year’s Baseball extravaganza; the other side of the dilemma is under fitting a model (high bias) which stems from wrong assumptions and fitting a overly simplistic model which does not describe the predictive outcome or target well enough.

Here is the segment to listen to below: